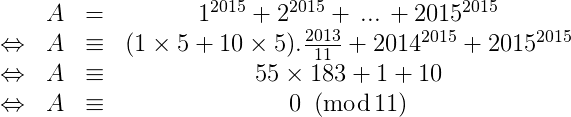Bài giải:

Ta chia thành các nhóm sau để tìm dư:

 Nhóm 1: Các số từ 1 tới 11, nhưng vì \(1^{2015}\) chia hết cho 11 nên thực chất ta chỉ xét từ 1 tới 10.

Nhóm 2: Các số từ 12 tới 22,  và cũng tương tự, ta chỉ xét tới 21.

...v.v

Số nhóm cần tách là: 2015Qa11= = 183 nhóm.

Mặt khác ta có công thức sau:

\((a+b)^n\equiv b^n\,(\text{mod }a\,\,\,(a>0)\)

Ta đi tính dư:

\(\begin{cases}1^{2015}\equiv1 & (\text{mod}\,11)\\2^{2015}\equiv10 & (\text{mod}\,11)\\3^{2015}\equiv1 & (\text{mod}\,11)\\4^{2015}\equiv1 & (\text{mod}\,11)\\5^{2015}\equiv1 & (\text{mod}\,11)\\6^{2015}\equiv10 & (\text{mod}\,11)\\7^{2015}\equiv10 & (\text{mod}\,11)\\8^{2015}\equiv10 & (\text{mod}\,11)\\9^{2015}\equiv1 & (\text{mod}\,11)\\10^{2015}\equiv10 & (\text{mod}\,11)\end{cases}\)

Vậy: