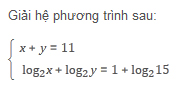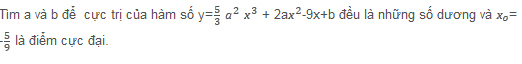Đồ thị của hàm số cắt

(A)Đường thẳng y=3 tại hai điểm

(B)Đường thẳng y=-4 tại hai điểm

(C)Đường thẳng $\frac{\mathrm{}}{\mathrm{}}$ tại ba điểm                       

(D)Trục hoành tại một điểm.

Tiếp tuyến của parabol $$ $$ tại điểm M(1;3) tạo với hai trục tọa độ một tam giác vuông. Diện tích tam giác đó là:

(A$\frac{\mathrm{}\mathrm{}}{\mathrm{}}$)                       (B)

(C)                         (D)

Tìm nghiệm gần đúng của phương trình f'(x)=0 với sai số tuyệt đối không vượt qua ${10}^{-4}$, biết :  f(x) = $x^3$-$x^2$-3x+1

(Trích bài 5.15/trang 181 sách BT ĐSGT 11(NC), Nguyễn Huy Đoan-Nguyễn Xuân Liêm-Nguyễn Khắc Minh-Đoàn Quỳnh-Ngô Xuân Sơn-ĐặngHùng Thắng-Lưu Xuân Tình)

Xét chiều biến thiên của hàm số sau:

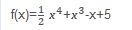
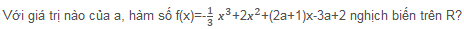
(Trich bài 1.8/ trang 11, sách BT Giải Tích 12(NC), Nguyễn Huy Đoan(cb) -Trần Phương Dung - Nguyễn Xuân Liêm - Phạm Thị Bạch Ngọc - Đoàn Quỳnh - Đặng Hùng Thắng)

Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 

(Trich bài 1.22/ trang 13, sách BT Giải Tích 12(NC), Nguyễn Huy Đoan(cb) -Trần Phương Dung - Nguyễn Xuân Liêm - Phạm Thị Bạch Ngọc - Đoàn Quỳnh - Đặng Hùng Thắng)

Tìm các hệ số a, b, c sao cho hàm số đạt cưc tiểu tại điềm x=1, f(1)=-3 và đồ thị hàm số cắt trục tung tại điểm có tung độ là 2.

Tìm các khoảng đơn điệu của hàm số 

( Bài 1/trang 45, sách Giải Tích 12,Trần Văn Hạo-Vũ Tuấn-Lê Thị Thiên Hương-

Nguyễn Tiến Tài-Cấn Văn Tuất, NXBGD 2008(sách in thử))